1ª FASE.- representa un método directo
para hacer coincidir ambas respuestas impulsionales. Desde un punto
revista de cálculo el método es difícil y no resulta
de utilidad.
2ª FASE.- a partir de los resultados vistos hasta
ahora se desarrolla una técnica de aproximación que es,
de hecho, mucho más práctica: Si la respuesta impulsional
del filtro analógico es \( h_a(t)\) digitalizamos esta respuesta
escribiendo:
Aún con todo surgen diversas dificultades:
1ª) pocos filtros analógicos se dan en términos
de una respuesta impulsional. Sí suelen expresar por su función
de transferencia o por su mapa de polos y ceros.
2ª) una vez obtenidos los \( h_k \) cuando el filtro que se
desea diseñar es recursivo, no resulta fácil deducir
sus coeficientes.
De todos modos existen algunos casos en los que se puede llegar a una
buena solución. Sea, por ejemplo, el problema de aproximar un integrador
analogico mediante un filtro digital recursivo. La respuesta general de
este filtro es:
\( \displaystyle y(t) = \int_{0}^{\tau} x(\tau)d\tau \)
Y su respuesta impulsional:
\( h_a(t) = \left\{
\begin{array}{l}
1\qquad si\quad t\geq 0 \\
\\
0\qquad si\quad t< 0 \\
\end{array}
\right. \)
La digitalización de \( h_a(t) \) nos da:
\( h_k = \left\{
\begin{array}{l}
1\qquad si\quad k\geq 0 \\
\\
0\qquad si\quad k< 0 \\
\end{array}
\right. \)
Afortunadamente, necesita calcular la transformada z de esta respuesta
impulsional, que ya hemos visto que viene dada por:
\( \displaystyle H(z) = \frac{z}{z-1} \)
Ya que se puede inferir de directamente del filtro qué no es más
que un integrador digital:
\( y_k = x_k + y_{k-1} \)
A continuación se presenta una técnica que no requiere el
cálculo de respuesta impulsional. Como en los filtros analógicos
se suele dar \( H_a(s) \) podemos calcular H(z) directamente de \( H_a(s)
\) evitando las complicaciones de la respuesta impulsional:
\( \displaystyle H_a(s) = \sum_{i=1}^{m}\frac{A_i}{s-p_i} \Rightarrow
h_a(t) = \sum_{i=1}^{m}h_{ai}(t) \)
Aplicando la transformada de Laplace podemos ver la respuesta impulsional
del i-ésimo de la descomposición en paralelo del filtro
\( H_a(s)\) es:
\( h_{ai}(t) =\left\{
\begin{array}{l}
A_i·\exp (p_it)\quad si\;t \geq 0 \\
\\
0\qquad\qquad\qquad si\;t < 0 \\
\end{array}
\right. \)
Y a partir de ahí:
\( \displaystyle h_k = h_a(kT) = \sum_{i=1}^{m}h_{ai}(kT) = \sum_{i=1}^{m}h_{ik}
= \sum_{i=1}^{m}A_i·\exp (p_ikT) \)
Por lo que tendremos:
\( \displaystyle h_{ik} = A_i·\exp (p_iT) \Rightarrow H_i(z)
= \sum_{k=0}^{\infty}A_i·\exp (p_1kT)·z^{-k} \)
Si se cumple que:
\( \displaystyle \frac{\exp(p_iT)}{z} < 1 \)
Tenemos una progresión geométrica convergente que da:
\( \displaystyle H_i(z) = \frac{A_i}{1 - \exp(p_iT)z^{-1}} = \frac{A_i·z}{z
- \exp(p_iT)} \)
Y finalmente:
\( \displaystyle H(z) = \sum_{i=0}^{m}H_i(z) = \sum_{i=0}^{m}\frac{A_i·z}{z
- \exp(p_iT)} \)
Hay muchos autores que multiplican esta función de transferencia
por \( z^{-1} \) adoptando:
\( \displaystyle H(z) = \sum_{i=1}^{m}\frac{A_i}{z - \exp(p_iT)} \)
Con lo que la expresión de \( h_k \) se desplaza una unidad de
periodo de tiempo:
La implementación gráfica de la aproximación realizada
queda reflejada en la figura adjunta
Todo lo anterior puede resumirse en el siguiente procedimiento de diseño:
Paso 1.- seleccionar un filtro analógico \( H_a(s) \)
Paso 2.- seleccionar el periodo de muestreo, T
Paso 3.- descomponer en paralelo la función de transferencia,
\( H_a(s) \)
\( \displaystyle H_a(s) = \sum_{i=1}^{m}\frac{A_i}{s - p_i } \)
Paso 4.- aproximar la respuesta impulsional de los filtros analógicos
de polo simple determinando filtros digitales cuyas respuestas impulsionales
sean los valores muestreados de las tres respuestas analógicas.
Esto se hace transformando los polos en el plano S en los polos en el
plano Z.
\( p_i \) en el plano \( s \rightarrow \exp (-p_iT) \) en el plano
z.
Cada filtro analógico se aproxima por un filtro digital collar
transformada Z es:
\( \displaystyle H_i(z) = \frac{A_i}{z - \exp (-p_iT)} \)
Paso 5.- calcular la transformada z del filtro digital que aproxima
al filtro analógico:
\( \displaystyle H(z) =\sum_{i=1}^{m} \frac{A_i}{z - \exp (-p_iT)}
\)
Paso 6.- realizar el filtro digital es cogiendo una forma (paralelo,
cascada,...) y calculando los coeficientes del filtro.
Los coeficientes de los filtros de la realización paralelas se
determinan directamente:
\( a_i = A_i \quad ;\quad b_i = \exp (-p_iT) \)
Ejemplo.- aproximar un integrador analogico mediante
un filtro digital cuya fuención de transferencia es:
\( \displaystyle H_a(s) = \frac{1}{s} \)
En filtro digital tiene un polo en z = 1 (independiente de T) por lo tanto:
\( \displaystyle H(z) = \frac{1}{z-1}= \frac{z^{-1}}{1 - z^{-1}} \Rightarrow
y_k = x_{k-1} + y_{k-1} \)
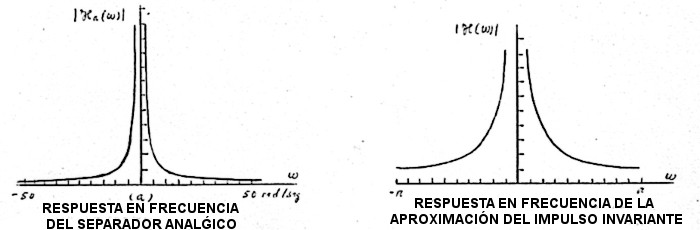
La respuesta en frecuencia del filtro analógico y su aproximación
digital están dadas en las figuras adjuntas.
Ejemplo.- aproximar un filtro de Butterworth paso- baja
de 3 polos con una frecuencia de corte de 10 rad/seg., y:
\( p_1 = 10/\underline{120º}\quad ; \quad p_2 = 10/\underline{180º}\quad
; \quad p_3 = 10/\underline{240º} \)
Suponer T = 0,05 seg.
Respuesta.- en primer lugar escribimos los tonos como
valores complejos:
\( p_i = \rho·e^{j\alpha} \Rightarrow p_1 = -5 + j·8,66
\; ;\; p_2 = -10 \; ;\; p_3 = -5 - j·8,66 \)
De ese modo, la función de transferencia será:
\( \displaystyle H_a(s) = \frac{1}{[s-(-5 + j·8,66)](s+10)[s-(-5
- j·8,66)]} \)
Descomponiendo en fracciones simples esta función obtenemos:
\( \displaystyle H_a(s) = 10^{-3}\left(\frac{-5- j·2,88}{s+5-j·8,66}
+ \frac{-5+ j·2,88}{s+5+j·8,66} + \frac{10}{s+10}\right)
\)
La transformación de los polos en el plano S a los polos en el
plano Z nos da:
\( \begin{array}{l}
\exp(-5 + j·8,66)(0,05) = 0,7788 /\underline{24,8º} = 0,707
+ j·0,327 \\
\\
\exp (-10)(0,05) = 0,6065 \\
\\
\exp(-5 - j·8,66)(0,05) = 0,7788 /\underline{-24,8º} = 0,707
- j·0,327
\end{array} \)
El mapa de polos y ceros para el filtro digital es el de la figura adjunta
y su función de transferencia será:
\( \displaystyle \begin{array}{l}
H(z) = \frac{0,00577/\underline{210º}}{z - 0,7788 /\underline{24,88º}}+
\frac{0.01}{z - 0,6065} \\
\\
\frac{0,00577/\underline{150º}}{z - 0,7788 /\underline{-24,88º}}
= \frac{10^{-4}(8,7·z + 6,365)}{z^3 - 2,02z^2 + 1,46z - 0,368}
\end{array}\)
Ejemplo.- resolver el mismo problema que antes con T = 0,1
Las de la formación de los polos nos da:
\( \begin{array}{l}
p_1 = \exp (-5+j·8,66)(0,1)= 0,6060/\underline{49,6º} \\
\\
P_2 = \exp (-10)(0,1) = 0,3697 \\
\\
p_1 = \exp (-5-j·8,66)(0,1)= 0,6060/\underline{-49,6º}
\end{array} \)
Y su mapa de polos y ceros (con solo los polos) es el de la figura adjunta
Comparando este mapa con el interior podemos observar que cuanto mayor
es T más se acercan los polos al origen y mayores se hacen sus
ángulos.
Teniendo en cuenta que los ceros de este filtro son los mismos que los
del anterior, resulta la función de transferencia:
\( \displaystyle H(z) = \frac{10^{-3}(2,411·z + 1,248)}{z^3 -
1,153·z^2 + 0,6561·z - 0,1351} \)
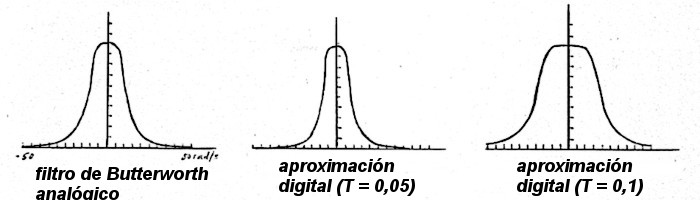
En la figura adjunta representa la respuesta en frecuencia para el filtro
de Butterworth analógico y las dos aproximaciones digitales estudiadas
Se observa que la segunda aproximación (derecha) no es tan buena
como la primera.