CAPÍTULO 7.- GRAFICOS DE CONTROL POR
VARIABLES
Gráfico basado en estudio inicial
A.- Gráfico de
la media
B.-
Gráfico del
recorrido
Gráficos basados
en valores standar
Gráficos de
control para valores individuales
Líneas generales
para el diseño del grafico \(\overline{X}\)
,R
Eficacia de los gráficos
\(\overline{X}\)
,R
Gráficos de control de sumas acumuladas
(CUSUM)
Los gráficos de control que hemos visto
hasta ahora se conocen como gráficos de
Shewhart. Un punto débil de los gráficos
de Shewhart es que solo se utiliza la información
contenida en la última muestra representada
e ignora la información dada por el conjunto
de muestras. Es cierto que la incorporación
de límites de atención y el estudio
de pautas trata de mejorar la sensibilidad del
gráfico Shewhart utilizando más
el conjunto de la información pero a costa
de complicar algo el gráfico reduciendo
la sencillez de la Interpretación
El gráfico de sumas acumuladas (CUSUM) se presenta como
una alternativa al grafico de Shewhart. Incorpora directamente
toda la información representando las sumas acumuladas
de las desviaciones de los valores muestrales respecto de un
valor objetivo. Por ejemplo, supongamos que se toman muestras
de tamaño igual o mayor que 1, siendo \( \overline{X}_i
\) la media muestral de la muestra i.
Si suponemos que μo es el objetivo
para la media del proceso, el gráfico de sumas acumuladas
se formará representando la cantidad \( S_m = \sum \Big(\overline{X}_i
- \mu_0 \Big )\) respecto al número de orden (m) de la
muestra.
Por combinar la información de varias muestras,
los gráficos de sumas acumuladas son más
efectivos que los gráficos de Shewhart
para detectar pequeños cambios. Son particularmente
eficaces cuando el tamaño de muestra es
n = 1 y, por consiguiente, adecuados para su utilización
cuando la tecnología permite inspeccionar
y medir cada unidad producida usando a la vez
un microordenador en el puesto de trabajo.
Si el proceso se mantiene bajo control en el objetivo μo
, la suma acumulable \( S_m = \sum \Big(\overline{X}_i - \mu_0
\Big )\) variará aleatoriamente respecto del valor cero.
Sin embargo, si la media asciende a μ1
> μo se apreciará una
tendencia ascendente en la suma acumulada Sm. Por
el contrario, si la media se desplaza a μ2
< μo se apreciara una tendencia
decreciente en Sm. Por consiguiente, una tendencia
determinada (positiva o negativa) se considerará como
una evidencia de que la media del proceso se ha desplazado debido
a la presencia de alguna causa asignable que hay que investigar
y eliminar.
Existen dos criterios para establecer formalmente
que el proceso está fuera de control. Uno
de ellos es un procedimiento gráfico: La
máscara V propuesta por Barnhard en 1959
y otro es un procedimiento numérico muy
adecuado para establecer en conjunción
con un microordenador. Aquí veremos este
segundo procedimiento.
En cada toma de muestra hay que calcular los 2
valores siguientes :
\( S_i = \sum \limits_{i=1}^l [\overline{X}_i - (\mu_0 + F)]
\quad ; \quad T_i = \sum \limits_{i=1}^l [\overline{X}_i -
(\mu_0 - F)] \)
donde:
\( \overline {X}\) es la media muestral en la toma i-ésima.
μo es el valor objetivo (media
centrada)
F es un parámetro de la carta de control que normalmente
vale δo/2 siendo δo
el cambio que queremos detectar con prontitud.
\( F = fˇ \sigma_{\overline{X}} = (f/\sqrt{n})ˇ \sigma\), siendo
normalmente f = 0,5 ya que queremos detectar normalmente cambios
del orden de \( \sigma_{\overline{X}}\) (n es el tamaño
muestral).Como veremos más adelante, F se puede seleccionar
también en algún juego de cartas ARL.
Cuando algún valor Si ó Ti
cumple que Si > H ó Ti <
-H (H elegido de acuerdo a la curva ARL que nos interese \(H
= h ˇ \sigma_{\overline{X}}\) siendo h normalmente 5) el proceso
se considera fuera de control. Si Si se hace negativo
o se pone a 0, de igual forma si Ti se hace positivo
o se pone a 0.
Una vez corregido el proceso los contadores Si
y Ti se pondrían a 0.
Las curvas ARL de los gráficos CUSUM, se
calculan a partir de los parámetros del
grafico, h y f (y del tamaño de la muestra,
que está implícito en el desplazamiento)
utilizando cadenas de Markov.
En la tabla 2.3 se dan valores de h y f más
comunes en función del desplazamiento de
la media a detectar y sus curvas ARL.
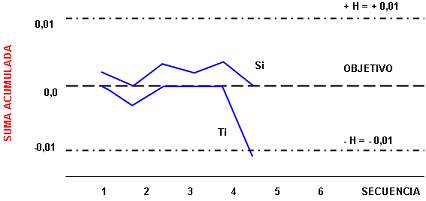
Ejemplo CUSUM
Consideremos que el peso de cartuchos de cierta fabricación
sigue siendo una distribución Normal (ver
ejemplo anterior) de media 1,3917 y desviación
típica 0,005. Valores que resultaban cuando
el proceso estaba bajo control.
\( \displaystyle \sigma_4 \frac{\overline{R}_4}{d_2} = 0,005
\)
Si utilizamos las muestras de tamaño 5 del
ejemplo anterior y queremos detectar desplazamientos de la medía
del orden de \( \sigma_{\overline{X}} = 0,0005 / \sqrt{5} =
0,0022 \), elejimos h = 5 y f = 0,5 con lo que obtenemos
F = 0,5 x 0,0022 = 0,0011 ; H = 5 x 0,0022 = 0,01
\( \scriptstyle \begin{array}{|c|c|c|c|c|c|} \hline & & LIM
\;SUP& (S_f < H) & LIM\; INF & (T_f < H) \\ \hline Secuencia
\; t & X_t & X_t - 1,3928 & S_t = \sum (X_t - 1,3928) & X_t
- 1,3906 & T_t = \sum /(X_t - 1,3906) \\ \hline 1 & 1,3948
& + 0,0020 & 0,0020 & + 0,0042 & > \\ \hline 2 & 1,3874 &
- 0,0054 & < 0 & - 0,0032 & - 0,0032 \\ \hline 3 & 1,3963
& + 0,0035 & 0,0035 & + 0,0057 & > 0 \\ \hline 4 & 1,3912
& - 0,0016 & 0,0019 & + 0,0006 & > 0 \\ \hline 5 & 1,3946
& + 0,0018 & 0,0037 & + 0,0004 & > 0 \\ \hline 6 & 1,3800
& - 0,0128 & < 0 & - 0,0106 & - 0,0106 \\ \hline \hline \end{array}
\)
En el sexto subgrupo \(T_i < - 0,01 \) por lo tanto es un
punto fuera de control y deberíamos corregir el proceso.
Para controlar la variabilidad dentro de las muestras
se pueden utilizar los gráficos de Shewart
del recorrido o de la desviación típica,
en conjunción con el CUSUM de medias.
No obstante también es posible diseñar
una carta de control CUSUM específicamente
por los gráficos de recorridos o de desviaciones
típicas. La forma de realizarlos es muy
similar al CUSUM de medias. Los parámetros
h y f con sus curvas ARL del CUSUM para recorridos
o desviaciones típicas están recogidos
en la norma británica BS 5703.
\( C_i = \sum \limits _{i=1}^i(R_i - F) \textrm{ donde } F = fˇ \overline{R}_T\)
TABLA 2.3
Valores de h y f recomendados para detectar un desplazamiento
de la media de magnitud \( \sigma / \sqrt{n}\) (*)
Otros gráficos
de control.- Gráfico de control de media móvil
Tablas para la elaboración
de gráficos de control
|